Convex Optimization
10. Convex Optimization#
This chapter provides general introduction to convex optimization problems. Convex optimization focuses on a special class of mathematical optimization problems where:
The real valued function being optimized (maximized or minimized) is convex.
The feasible set of values for the function is a closed convex set.
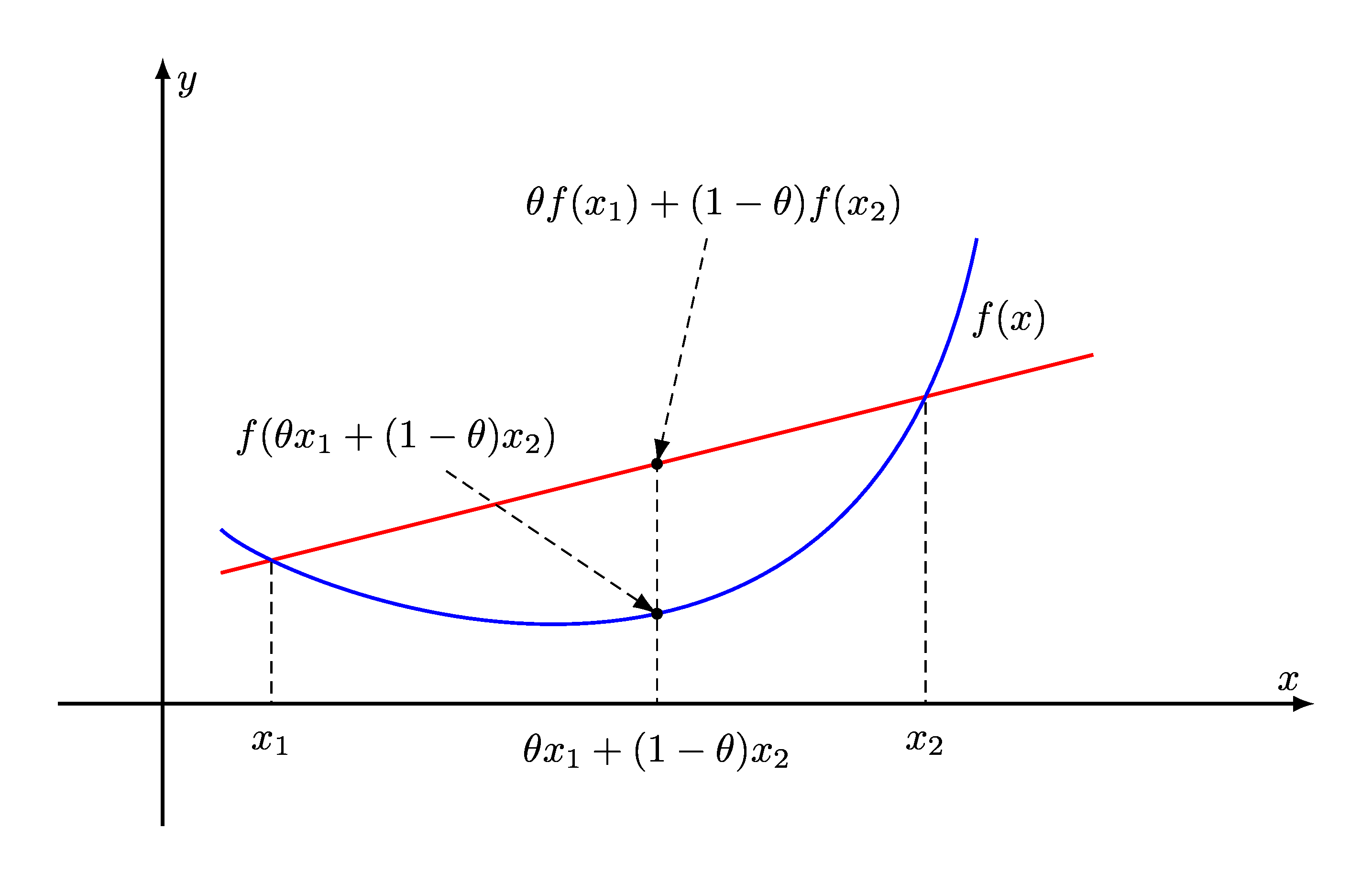
Fig. 10.1 For a convex function, the line segment between any two points on the graph of the function does not lie below the graph between the two points. Its epigraph is a convex set. A local minimum of a convex function is also a global minimum.#
Convex optimization problems are usually further classified into
Least squares
Linear programming
Quadratic minimization with linear constraints
Quadratic minimization with convex quadratic constraints
Conic optimization
Geometric programming
Second order cone programming
Semidefinite programming
There are specialized algorithms available for each of these classes.
Some of the applications of convex optimization include:
Portfolio optimization
Worst case risk analysis
Compressive sensing
Statistical regression
Model fitting
Combinatorial Optimization